Neste artigo vou falar sobre como realizar cálculos de permutação, arranjo e combinação na calculadora científica.
As instruções aqui apresentadas são para as calculadoras nos modelos da CASIO FX-82MS, FX-83MS, FX-85MS, FX-270MS, FX-300MS e FX-350MS, mas alguns outros modelos não citados podem apresentar semelhanças.
Permutação e arranjo
No arranjo ou permutação a ordem dos elementos importa.
Vou começar falando sobre a permutação. Existem dois tipos, o primeiro é a permutação simples e o segundo a permutação com repetição.
De modo geral, a permutação realiza a troca de lugares entre os elementos, é onde temos o caso de anagramas.
Para realizar cálculos de permutação utilizamos o fatorial.
Para chamar a função fatorial utilizamos a tecla x! que está em amarelo acima do botão $x ^ {-1}$.
Permutação
Quando o grupo não possui repetição de elementos dizemos que é uma permutação simples e sua equação é n!, onde n é a quantidade de elementos.
Ex.: permutação do conjunto de elementos B = {a, b, c}.
Possuímos 3 elementos e para permutar entre eles digitamos na calculadora 3, SHIFT, x!

Ao pressionar a tecla igual descobrimos que podemos escrever de 6 formas os elementos do conjunto B apenas trocando eles de lugares.
| abc, acb, bca, bac, cab e cba |
Já quando os elementos do grupo que desejamos permutar possuem repetição chamamos de permutação com repetição e sua equação é a da imagem abaixo, onde α, β… é a quantidade de cada elemento que se repete.
$$ P^{\alpha,\beta,…}_n = \frac{n!}{\alpha! \times \beta! \times…} $$
Ex.: Anagrama da palavra MATEMÁTICA.
Podemos ver que as letras M, A e T se repetem, sendo que M se repete duas vezes, A três vezes e T duas vezes.
Então a expressão para resolver este anagrama é:
$$ P^{2,3,2}_{10} = \frac{10!}{2! \times 3! \times 2!} $$
Na calculadora escrevemos:

Obtemos então que a quantidade de anagramas possíveis para a palavra MATEMÁTICA é de 151.200.
Arranjo
Primeiramente vamos falar sobre o arranjo simples.
Ele acontece quando existe um conjunto com n elementos que são diferentes entre eles, e estes elementos são dispostos em um grupo com uma determinada quantidade r de posições.
Onde r deve ser menor ou igual a quantidade de elementos.
A equação utilizada para calcular arranjo simples é:
$$ A^n_r = \frac{n!}{(n-r)!} $$
Onde n é a quantidade de elementos e r o número de elementos de cada grupo.
Na calculadora utilizamos a função nPr que está em amarelo acima da tecla nCr.
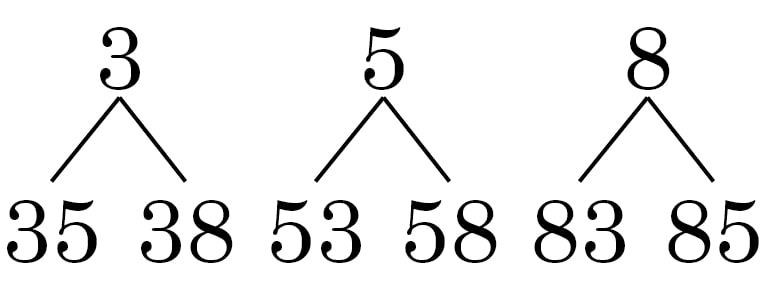
Ex.: Dado o conjunto $A = {3, 5, 8}$, escreva todos os números de dois algarismos distintos com os elementos de A.
A equação é:
$$ A^3_2 = \frac{3!}{(3-2)!} $$
Então na calculadora escrevemos:

Primeiro digitamos o valor de n, segundo chamamos a função nPr e por último digitamos o valor de $ r $.
Então, podemos escrever com os elementos de A, 6 números de dois algarismos distintos, em que cada grupo difere do outro, seja pelos elementos ou pela disposição entre eles:
Mas agora vamos falar sobre os arranjos com repetição.
Definimos arranjos com repetição o arranjo de n elementos diferentes com repetição e r posições, e a sua equação é:
$$ (AR)_{n,r} = n^r $$
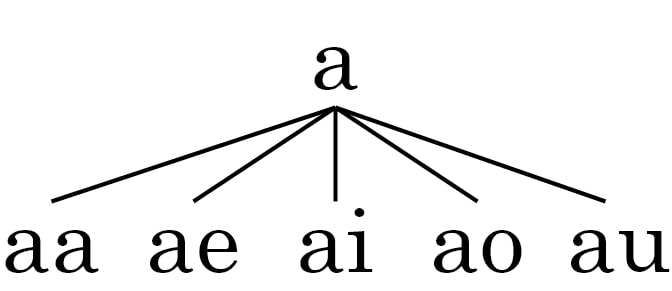
Ex.: Considere o conjunto das vogais, quantos arranjos com repetição podemos formar utilizando apenas duas vogais?
Temos então 5 vogais e 2 posições que podem ser utilizadas, ou seja:

Obtemos o resultado 25 arranjos possíveis.
Combinação
Quando falamos de combinação, diferente de arranjo e permutação, a ordem que os elementos estão dispostos não importa.
Por exemplo, combinar as cores azul e amarelo para formar a cor verde. Tanto faz se você coloca o azul ou o amarelo primeiro, o resultado vai ser o mesmo, a cor verde.
A combinação pode ser representada como binômio de Newton, ou:
$$ C_{n,r} = \frac{n!}{r!(n-r)!} $$
Onde n é a quantidade de elementos e r o número de elementos em cada grupo.
Ex.: Com um grupo de 4 pessoas, quantas comissões de 2 pessoas podemos formar?
Temos então:
$$ C_{4,2} = \frac{2!}{r!(4-2)!} $$
Na calculadora utilizamos a função nCr.
Primeiro digitamos o valor de n, segundo chamamos a função nCr e por último digitamos o valor de r.

Podemos ver então que conseguimos formar 6 comissões diferentes.

Gostou e acha que vai ajudar mais alguém? Então compartilhe.
Tem alguma dúvida? Deixa aqui nos comentários ou pode vir falar comigo pelas redes sociais, os links estão no rodapé do site.